The measure of each interior angle of a regular polygon is 144 . Michaela used the fact that the sum of the exterior angles of any polygon is 360 to show that the polygon has 10 sides. Her steps are as follows:
| Step 1 | The sum of the exterior angles = 360° |
| Step 2 | The measure of each exterior angle = 360° n |
| Step 3 | 360° n = 180° – 144° |
| Step 4 | 360° n = 36° |
| Step 5 | 360° = 36°n |
| Step 6 | 10 = n |
If the teacher asks Michaela to justify her reasoning for the third step, what should Michaela answer?
A. Each exterior angle is supplementary with an interior angle.
Correct! An exterior angle and its adjacent interior angle form a linear pair, and linear pairs of angles are always supplementary.
B. The sum of the angle measures is 180°.
Incorrect. The sum of the angle measures for a triangle is 180°.
C. Each exterior angle is complementary with an interior angle.
Incorrect. Each exterior angle is complementary wtih its respective interior angle.
D. 180° is one-half of 360°.
Incorrect. Let n represent the number of sides of the polygon.
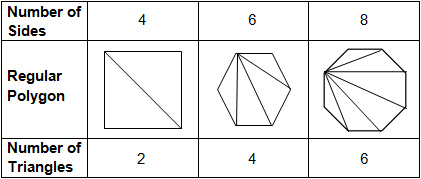
The table below shows how many triangles are formed when all the diagonals are drawn from one vertex in different regular polygons.

Based on the information in the table, which of the following statements is true?
A. The number of triangles formed in any regular polygon is 2 less than the number of sides in the polygon.
Correct! The pattern here reflects that there are 2 fewer triangles in each figure than there are sides in the polygon.
B. The number of triangles formed in any regular polygon is half the number of sides in the polygon.
Incorrect. Recount the number of sides and then number of triangles in each polygon above.
C. All the triangles formed in each regular polygon are congruent.
Incorrect. Look at the triangles formed in the hexagon and octagon in the table above.
D. All the triangles formed in each regular polygon are isosceles.
Incorrect. An isosceles triangle has at least two congruent sides.
Look at the NASA logo shown below. The logo has the shape of a regular decagon with all of the interior angles congruent and all of the sides congruent. Which of the following conjectures could not be made from the figure and the properties of a regular decagon?

A. Each of the 10 sides of the decagon are congruent.
Incorrect. This is a true statement, since a decagon has 10 sides, and a regular decagon has 10 congruent sides.
B. The measure of one exterior angle of this log is 36°.
Incorrect. This is a true statement, since the sum of the exterior angles of any polygon is 360°.
C. If all of the diagonals were drawn from one vertex in this figure, there would be 10 diagonals from that vertex.
Correct! From any one vertex, there are 3 fewer diagonals than there are vertices in the polygon.
D. If all of the diagonals were drawn from one vertex in this figure, there would be 8 triangles contained inside the decagon.
Incorrect. This is a true statement, since there are 2 fewer triangles than the number of sides contained inside any polygon.
The set of figures below is divided into two groups: figures that are polygons and figures that are not polygons.
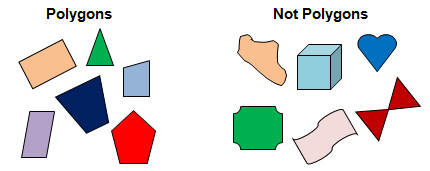
Which of the following conjectures can be made from the sets of figures?
A. Polygons must have 4 sides.
Incorrect. There are figures in the polygons set that have more than 4 or less than 4 sides.
B. Polygons cannot have curved sides.
Correct! This is one of the attributes of a polygon.
C. If a figure is green, it must be a polygon.
Incorrect. There are green figures in each set.
D. Whether or not a figure is a polygon, all figures are flat.
Incorrect. The set of figures that are not polygons contains a cube, which is a 3-dimensional object.